In this article, we will learn How to use the Z.TEST function in Excel.
What is hypothesis testing and how to use Z -Test for hypothesis testing ?
In statistics, Hypothesis testing is used to find the estimation of mean for the population dataset using the different distribution function based on the part of population dataset named sample dataset. A statistical hypothesis, sometimes called confirmatory data analysis, is a hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables. There are two types of hypothesis. One is null hypothesis which is the claimed statement and other is the alternate hypothesis which is just opposite of the null hypothesis. For example if we say maximum limit to lead in a maggi packet must not exceed 225 ppm (parts per million) and someone claims that there is more than fixed limit than null hypothesis (denoted by U0 ) and the alternate hypothesis (denoted by Ua )
U0 = lead content in maggi packet is more than or equal to 225ppm.
Ua = lead content in maggi packet is less than 225 ppm.
So the above hypothesis is an example of a right-tailed test as the underlying situation lies in the right side of the distribution curve. If the underlying situation lies on the left side then it would be called a left-tailed test. Let's take one more example which illustrates a one-tailed test. For example if selina said she can do 60 push ups on an average. Now you might doubt that statement and try to hypothesize the situation in statistics term then, the null and the alternate hypothesis is stated below
U0 = selina can do 60 pushups
Ua = selina cannot do 60 pushups
This is a two-tailed test where the underlying situation lies on both sides of the claimed statement. These tailed tests affect the outcome of the statistics. So choose the null and alternative hypothesis carefully.
Z - Test
A Z-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution. Z-test tests the mean of a distribution in which we already know the population variance. Because of the central limit theorem, many test statistics are approximately normally distributed for large samples. The test statistic is assumed to have a normal distribution such as standard deviation should be known in order for an accurate z-test to be performed. For example an investor wishes to test whether the average daily return of a stock is greater than 1% can be evaluated using Z test. A Z-statistic or Z-score is a number representing how many standard deviations above or below the mean population a score derived from a Z-test is. Mathematically first we decide the null hypothesis and calculate the Z score for the distribution using the formula.

Here
X (with a bar) is the mean of the sample array
U0 is the estimate population mean
s is the standard deviation where s is equal to std/(n)1/2 (where n is sample size).
As stated above Z - test follows standard normal distribution. So mathematically in Excel it follows the following formula.
Z.TEST( array,x,sigma ) = 1- Norm.S.Dist ((Average(array)- x) / (sigma/(n)1/2),TRUE)
or when sigma is omitted:
Z.TEST( array,x ) = 1- Norm.S.Dist ((Average(array)- x) / (STDEV(array)/(n)1/2),TRUE)
where x is the sample mean AVERAGE(array), and n is COUNT(array).
Let's learn how to do the Z test using the Z.TEST function to calculate the relation between the two given datasets (actual and observed).
Z.TEST Function in Excel
The Z.TEST function returns the probability that the sample mean would be greater than the average of observations in the data set (array). The function takes the following arguments.
Z.TEST Function syntax for one tailed probability:
| =Z.TEST ( array , x , [sigma] ) |
The function can also be used to commute two-tailed probability.
Z.TEST Function syntax for one tailed probability:
| =2 * MIN(Z.TEST ( array , x , [sigma] ), 1-Z.TEST ( array , x , [sigma] ) ) |
array : sample data distribution
x : value for which z test is evaluated
[sigma] : [optional] The population (known) standard deviation. If omitted, the sample standard deviation is used.
Example :
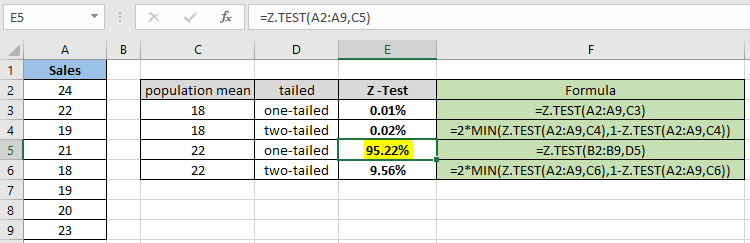
All of these might be confusing to understand. Let's understand how to use the function using an example. Here we have a sample dataset Sales and we need to find the Z test probability for the given hypothesized population mean assuming one tailed test.
Use the formula:
| = Z.TEST( A2:A9 , C3 ) |

The probability value comes in decimal, so you can convert the value to percentage changing the format of the cell to percentage.

As you can see the probability value for the hypothesized population mean 18 comes out to be 0.012% for the one tailed distribution.
Now calculate the probability assuming two tailed distributions having the same parameters.
Use the formula:
| = 2 * MIN( Z.TEST(A2:A9,C4) , 1 - Z.TEST(A2:A9,C4) ) |

For the two tailed distribution the probability gets doubled for the same sample dataset. So it's necessary to check the null hypothesis and alternate hypothesis.
Now calculate the probability for the different hypothesized population mean and one tailed distribution.
Use the formula:
| = Z.TEST( A2:A9 , C5 ) |
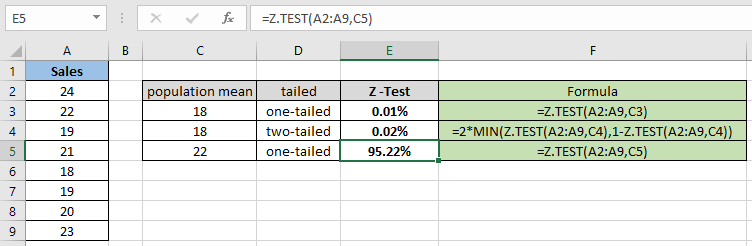
As you can see the probability value for the hypothesized population mean 22 comes out to be 95.22% for the one tailed distribution.
Now calculate the probability assuming two tailed distributions having the same parameters.
Use the formula:
| = 2 * MIN( Z.TEST(A2:A9,C6) , 1 - Z.TEST(A2:A9,C6) ) |

As you can differ from the above snapshot that the probability value gets less when calculating the two tailed distribution. The function returns 9.56% for the hypothesized population mean 22.
Z.TEST represents the probability that the sample mean would be greater than the observed value AVERAGE(array), when the underlying population mean is 0. From the symmetry of the Normal distribution, if AVERAGE(array) < x, Z.TEST will return a value greater than 0.5.
Here are all the observational notes using the Z.TEST function in Excel
Notes :
Hope this article about How to use the Z.TEST function in Excel is explanatory. Find more articles on statistical formulas and related Excel functions here. If you liked our blogs, share it with your friends on Facebook. And also you can follow us on Twitter and Facebook. We would love to hear from you, do let us know how we can improve, complement or innovate our work and make it better for you. Write to us at info@exceltip.com.
Related Articles :
How To Use Excel T TEST Function in Excel : The T.TEST is used to determine the confidence of an analysis. Mathematically, it is used to know if the mean of the two samples are equal or not. T.TEST is used to accept or reject the null hypothesis.
How to use Excel F.TEST Function in Excel : The F.TEST Function is used to calculate F statistic of two samples in excel internally and returns the two tailed probability of the F statistic under Null Hypothesis.
How to use the DEVSQ Function in Excel : DEVSQ function is a built-in statistical function to calculate the sum of squared deviations from the mean or average of the range of data values provided.
How to use Excel NORM.DIST Function : Calculate the Z score for the normal cumulative distribution for the pre specified values using the NORMDIST function in Excel.
How to use Excel NORM.INV Function : Calculate the inverse of Z score for the normal cumulative distribution for the pre-specified probability values using the NORM.INV function in Excel.
How to Calculate Standard Deviation in Excel : To calculate the standard deviation we have different functions in Excel. The standard deviation is the square root of the variance value but It tells more about the dataset than variance.
How to use the VAR function in Excel : Calculate the variance for the sample dataset in excel using the VAR function in Excel.
Popular Articles :
How to use the IF Function in Excel : The IF statement in Excel checks the condition and returns a specific value if the condition is TRUE or returns another specific value if FALSE.
How to use the VLOOKUP Function in Excel : This is one of the most used and popular functions of excel that is used to lookup value from different ranges and sheets.
How to use the SUMIF Function in Excel : This is another dashboard essential function. This helps you sum up values on specific conditions.
How to use the COUNTIF Function in Excel : Count values with conditions using this amazing function. You don't need to filter your data to count specific values. Countif function is essential to prepare your dashboard.
The applications/code on this site are distributed as is and without warranties or liability. In no event shall the owner of the copyrights, or the authors of the applications/code be liable for any loss of profit, any problems or any damage resulting from the use or evaluation of the applications/code.