The Excel REPT function is a simple function, that prints a given text to given times. In this article, we will explore how REPT function works, how REPT functions can be used, and where REPT function is used best, what tricks can be done using this function. There’s so much, just keep reading.
REPT Function Syntax
Text: The characters/s you want to repeat.
Number: The number of times you want to repeat a given text.
For example, if I want to print “HA” three times, I will write REPT formula as shown below.
The formula above will return “HAHAHA” as a result. Now at this point, The REPT function doesn’t sound very useful. But wait, it is more useful than it sounds. See below use cases of Excel REPT function.
Excel REPT Function for In Cell Bar Chart
I know that, you can create in cell bar charts using conditional formatting options. But they have their own limitations. Like you cant change color based on condition.
So for any given reason, if you want to create a progress bar chart in a cell, follow below example.
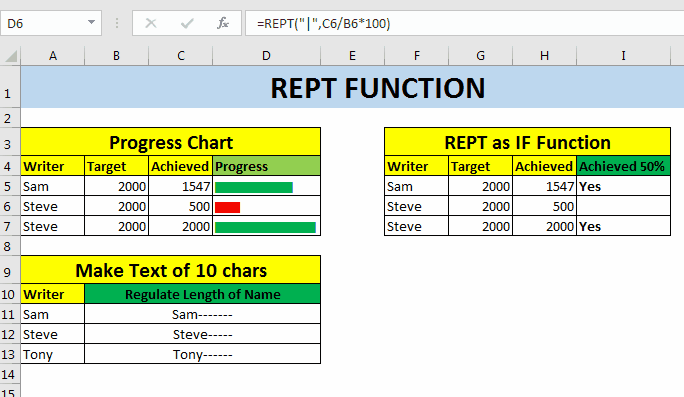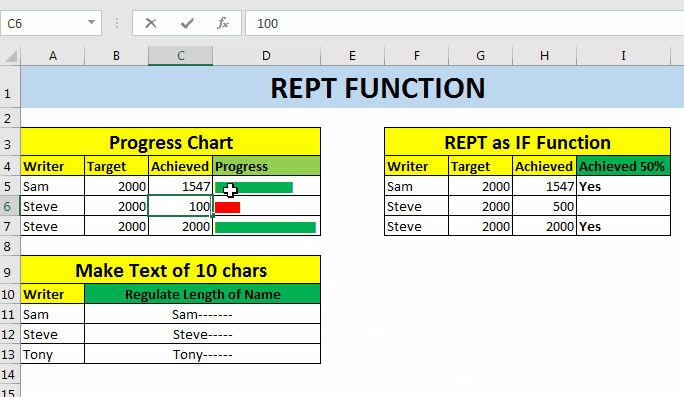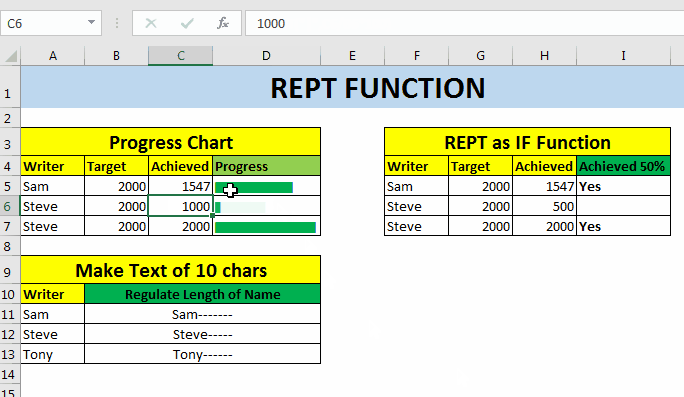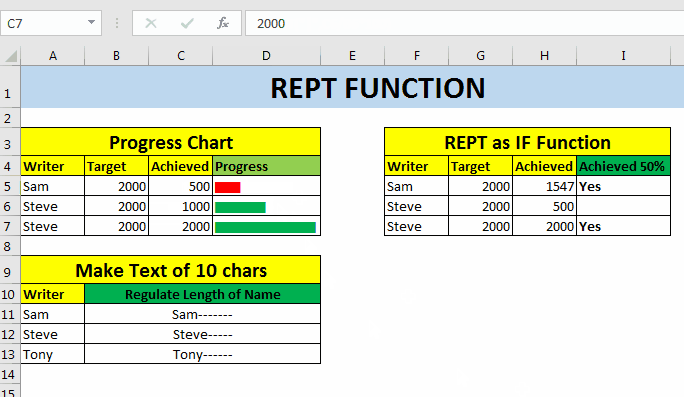
In-cell bar chart using REPT function
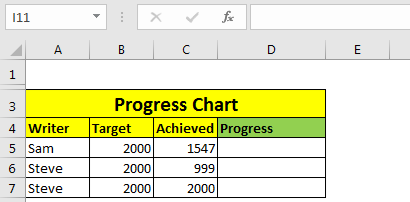
I have this data, that shows the target and achievement of the writers on exceltip.com. In column D, we will use REPT function to create a bar that shows the progress of writers. The progress bar is of % achievement.
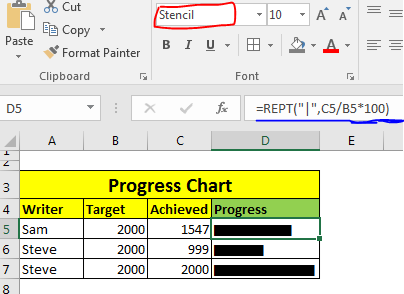
=REPT("|",C5/B5*100)
And now you have a bar chart that shows the progress of writers in one cell. All this you’ve done using REPT function of Excel.
Now if you want to color these bars on some conditions, you can use conditional formatting too. For example here, I have I want to bar to be red if it’s less then 50%, else Green. So I need to apply conditional formatting based on formula (if<50% and if>=50%).
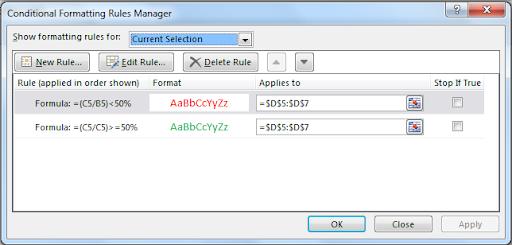
Finally I will have this bar chart created using REPT function.

Note: If you supply a fraction number to REPT function, it will be truncated. For example if you supply 50.92, it will make it 50. If you want to round it to closest value, Use ROUND function.
Repeat Formula in Excel to Print on a Condition
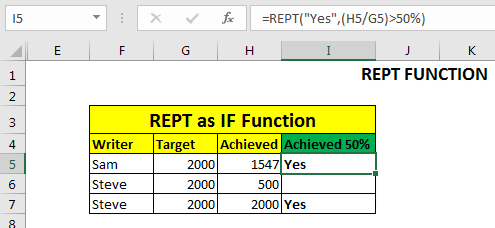
You can use REPT function to print something based on a condition, similar to Excel IF Function. Let’s see this example.
In this example, I have same data as above, but instead of progress bar, I want to print “Yes” if a writer has achieved 50% of his target.

So, in cell I5 write this Repeat Formula, and copy down the cells.
This will give us the desired result as shown below.
How It Works?
Actually, This Repeat function converts boolean values into number. True is 1 and False is 0. So when if given condition is True, it prints the given string one time. If false it prints the given string zero times, means nothing is printed. The above function is equivalent to =IF((H5/G5)>50%,”Yes”,””).
Note: It is kind of obvious but still, If you supply 0 as repetition number of text,nothing will be printed.
REPT Function to Maintain Text Length For this example, let’s assume that we get name of candidates in cell. For any purpose, we want text to be length of at least 20. If any name is less then 20 characters, we will ad remaining letters as -- after the name. If you know about LEN function of excel, you’ve must figured out to how to do this. I am explaining it here, anyway.Here I have some names. And I want to add hyphen (-) after the name and repeat it to remaining letters. The formula is simple, write the name first, then count characters in name and subtract it from 10.
Write this REPT Formula in cell B11, and copy in below cells.
This will give us the desired result.

So, yeah guys, this is the REPT function that is also called Repeat function in excel. This is simple. Just repeats a string given times. But in smart hands this can be used as very powerful function. This can be used to create really impressive dashboards.
If you know any amazing use of this function, or of any other excel function in excel, let us know in the comments section below. Or if you have any doubt about this function, you can ask that too.
Articles other visitors visited:
Excel Sparklines : The Tiny Charts in Cell
How to use the IF function in Excel
Conditional Formatting with formula
How to Use REPLACE function in Excel
How to Use SUBSTITUTE function in Excel
Popular Articles
The applications/code on this site are distributed as is and without warranties or liability. In no event shall the owner of the copyrights, or the authors of the applications/code be liable for any loss of profit, any problems or any damage resulting from the use or evaluation of the applications/code.