The Excel STDEV.S Function is used to calculate the standard deviation in the sample data set. The S in STDEV.S stands for Sample. It is an updated version of STDEVS function in excel. Excel recommends the use of STDEV.S function over STDEVS function. This is also called unbiased analysis.

If you want to calculate the standard deviation of the entire population, use STDEV.P function.
What is the standard deviation? It is used to evaluate how far the data is spread from the mean of data sample. It is the squire root of variance.
Syntax of STDEV.S
Number1,number2,...: these are the number of which you want to calculate standard deviation.
The first number is compulsory.
The first argument in is compulsory, rest are optional.
These numbers can be supplied as individual numbers, cell references, ranges or arrays to STDEV.S function.
All below formulas are valid STDEV.S formulas.
STDEV.S Example
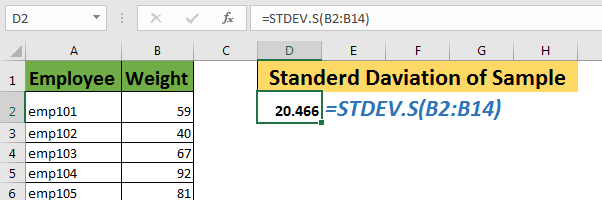
Here we have a data sample of weights of employees. We want to calculate the standard deviation to see how much the weights are spread over the average weights of these employees.

Write below STDEV.S formula in cell D2:
This will return standard deviation of around 20.5.

If we plot a graph with on 1 to 100 with this standard deviation, the standard deviation graph will look like something this.

If we calculate standard deviation using STDEV.P it will be slightly less. It will be 19.7.
The result of STDEV.S always greater than STDEV.P’s result on same data. You can see in below graph that standard deviation of sample is more spread than standard deviation of population.

STDEV.S vs STDEV.P
So, what is the difference in STDEV.S and STDEV.P function? Let’s Explore.
Since, STDEV.P function takes whole data, and some factors may dominate the result standard deviation. And Since it will be taken as the standard deviation for everyone in data, even for minorities, this is called Biased Analysis. This is why, this standard deviation is recommended to use only when analysis is non-destructive.
Important:
So yeah, this STDEV.S function. I hope this was informative. If you have any doubts or suggestion regarding this article or any other function of excel, be my guest and use comment section below. I will be more than happy to here from you guys.
Related Data:
How To Use STDEV.P Function in Excel
How to Use STDEV Function in Excel
Regressions Analysis in Excel
How To Calculate MODE function in Excel
How To Calculate Mean function in Excel
How to Create Standard Deviation Graph
Popular Articles:
50 Excel Shortcuts to Increase Your Productivity
How to use the VLOOKUP Function in Excel
The applications/code on this site are distributed as is and without warranties or liability. In no event shall the owner of the copyrights, or the authors of the applications/code be liable for any loss of profit, any problems or any damage resulting from the use or evaluation of the applications/code.