
In this article, we will learn How to use the TDIST function, T.DIST function, T.DIST.RT function and T.DIST.2T function in Excel.
What is hypothesis testing using T distribution and degree of freedom?
In statistics, Hypothesis testing is used to find the estimation of mean for the population dataset using the different distribution function based on the part of population dataset named sample dataset. A statistical hypothesis, sometimes called confirmatory data analysis, is a hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables. A statistical hypothesis test is a method of statistical inference. There are two types of hypothesis. One is null hypothesis which is the claimed statement and other is the alternate hypothesis which is just opposite of the null hypothesis. For example if we say maximum limit to lead in a maggi packet must not exceed 225 ppm (parts per million) and someone claims that there is more than fixed limit than null hypothesis (denoted by U0) and the alternate hypothesis (denoted by Ua)
U0 = lead content in maggi packet is more than or equal to 225ppm.
Ua = lead content in maggi packet is less than 225 ppm.
So the above hypothesis is an example of a right-tailed test as the underlying situation lies in the right side of the distribution curve. If the underlying situation lies on the left side then it would be called a left-tailed test. Let's take one more example which illustrates a one-tailed test. For example if selina said she can do 60 push ups on an average. Now you might doubt that statement and try to hypothesize the situation in statistics term then, the null and the alternate hypothesis is stated below
U0 = selina can do 60 pushups
Ua = selina cannot do 60 pushups
This is a two-tailed test where the underlying situation lies on both sides of the claimed statement. These tailed tests affect the outcome of the statistics. So choose the null and alternative hypothesis carefully. T distribution is a family of continuous probability distribution when estimating the mean of a normally distributed population in situations where the sample size is small (generally < 30) and the population standard deviation is unknown. T distribution is a bell shaped curve but much flatter than normal distribution curve. The T distribution function varies with degrees of freedom. Let's understand the cumulative distribution function for the t distribution with different degrees of freedom.

Here
2F1 is the hypergeometric function
x is the value at which the distribution is evaluated.
Now we look forward to the probability mass distribution for the t distribution. The variation of degree of freedom with probability distribution is shown with plot below.
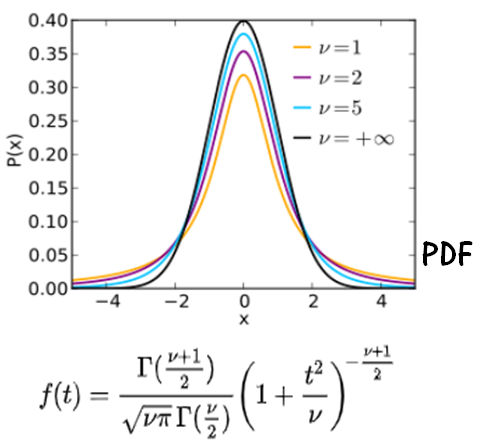
Here
x is the value at which the distribution is evaluated.
Degree of Freedom variable :
Now you must be wondering what is the degree of freedom (also known as df). Mathematically, the degree of freedom(df) of a distribution is equal to the number of standard normal deviations being summed. But how can we understand the concept of degree of freedom? Degree of freedom is the number of independent possibilities in an event. For example if we toss a coin 100 times and say heads occur 48 times and then we can conclude the tails occured 52 times so the degree of freedom is 1. But if we say on a route of traffic lights (generally has 3 color lights) we want to know the probability of red light in any given sample of time. For this the degree of freedom will be 2 as we will require information for at least 2 color lights. So the degree of freedom is the 1 - sample size of distribution. Let's learn how to evaluate t - distribution for the type of tailed test using the T.DIST or TDIST or T.DIST.2T or T.DIST.RT function probability for the variable x.
TDIST Function in Excel
The T.DIST function in Excel returns the t distribution probability percentage of something across samples, The function takes variable x and degrees of freedom for the distribution along with the type of tailed test.
TDIST Function syntax:
| =TDIST(x , deg_freedom ,tails) |
x : value at which distribution is evaluated
deg_freedom : degrees of freedom
Tails : one tailed (use 1) or two tailed (use 2) test
T.DIST.RT Function returns the right tailed distribution for the one tailed test using the variable x and deg of freedom.
T.DIST.RT Function syntax:
| =T.DIST.RT(x , deg_freedom) |
x : value at which distribution is evaluated
deg_freedom : degrees of freedom
T.DIST.2T Function returns the two-tailed test for the distribution using the variable x and deg of freedom.
T.DIST.2T Function syntax:
| =T.DIST.2T(x , deg_freedom) |
x : value at which distribution is evaluated
deg_freedom : degrees of freedom
T.DIST Function returns the student t distribution for the left tailed test using the variable x and deg of freedom along with the type of distribution (cdf or pdf)
T.DIST Function syntax:
| =T.DIST(x , deg_freedom ,tails) |
x : value at which distribution is evaluated
deg_freedom : degrees of freedom
cumulative : logical value that determines the form of the function. If cumulative is TRUE, T.DIST returns the cumulative distribution function; if FALSE, it returns the probability density function.
Example :
All of these might be confusing to understand. Let's understand how to use the function using an example. Here we have a sample variable x and degree of freedom. We need to calculate the probability percentage for the t distribution one tailed test using the TDIST function in Excel
Use the formula:
| =TDIST(B3 , B4 , 1) |

The probability value is in decimal you can convert the value to percentage changing the format of the cell to percentage.

The probability value of t distribution for exact 0.5 comes out to be 33.3% for the one tailed test.
Now use the same formula with the same parameters for the two tailed tests. Let's use the below stated formula.
Use the formula:
| =TDIST(B3 , B4 , 2) |

The probability value of t distribution for exact 0.5 comes out to be 66.67% for the two-tailed test.
Now evaluate the right tailed test for the same parameters using the T.DIST.RT function stated below.
Use the formula:
| =T.DIST.RT ( B3 , B4 ) |

The probability value of t distribution for exact 0.5 comes out to be 33.33% for the right-tailed test.
Now evaluate the two-tailed test for the same parameters using the T.DIST.RT function stated below.
Use the formula:
| =T.DIST.2T ( B3 , B4 ) |

The probability value of t distribution for exact 0.5 comes out to be 66.67% for the two-tailed test.
Now we use the T.DIST function to choose the type of cumulate function (cdf or pdf) with the same parameters.
Use the formula for the cdf:
| =T.DIST ( B3 , B4, TRUE ) |

The probability for the 0.5 value for the degree of freedom 2 comes out to be 66.67% for the left-tailed and cumulative distribution
Use the formula for the pdf:
| =T.DIST ( B3 , B4, FALSE ) |

The probability for the 0.5 value for the degree of freedom 2 comes out to be 29.63% right-tailed and probability mass distribution.
Here are all the observational notes using the T distribution functions in Excel
Notes :
Hope this article about How to use the TDIST function, T.DIST function , T.DIST.RT function and T.DIST.2T function in Excel is explanatory. Find more articles on statistical formulas and related Excel functions here. If you liked our blogs, share it with your friends on Facebook. And also you can follow us on Twitter and Facebook. We would love to hear from you, do let us know how we can improve, complement or innovate our work and make it better for you. Write to us at info@exceltip.com.
Related Articles :
How To Use Excel T TEST Function in Excel : The T.TEST is used to determine the confidence of an analysis. Mathematically, it is used to know if the mean of the two samples are equal or not. T.TEST is used to accept or reject the null hypothesis.
How to use Excel F.TEST Function in Excel : The F.TEST Function is used to calculate F statistic of two samples in excel internally and returns the two tailed probability of the F statistic under Null Hypothesis.
How to use the DEVSQ Function in Excel : DEVSQ function is a built-in statistical function to calculate the sum of squared deviations from the mean or average of the range of data values provided.
How to use Excel NORM.DIST Function : Calculate the Z score for the normal cumulative distribution for the pre specified values using the NORMDIST function in Excel.
How to use Excel NORM.INV Function : Calculate the inverse of Z score for the normal cumulative distribution for the pre-specified probability values using the NORM.INV function in Excel.
How to Calculate Standard Deviation in Excel : To calculate the standard deviation we have different functions in Excel. The standard deviation is the square root of the variance value but It tells more about the dataset than variance.
Regressions Analysis in Excel : Regression is an Analysis Tool, which we use for analyzing large amounts of data and making forecasts and predictions in Microsoft Excel.
How to Create Standard Deviation Graph : The standard deviation tells how much data is clustered around the average of the data. Learn how to create a standard deviation graph here.
How to use the VAR function in Excel : Calculate the variance for the sample dataset in excel using the VAR function in Excel.
Popular Articles :
How to use the IF Function in Excel : The IF statement in Excel checks the condition and returns a specific value if the condition is TRUE or returns another specific value if FALSE.
How to use the VLOOKUP Function in Excel : This is one of the most used and popular functions of excel that is used to lookup value from different ranges and sheets.
How to use the SUMIF Function in Excel : This is another dashboard essential function. This helps you sum up values on specific conditions.
How to use the COUNTIF Function in Excel : Count values with conditions using this amazing function. You don't need to filter your data to count specific values. Countif function is essential to prepare your dashboard.
The applications/code on this site are distributed as is and without warranties or liability. In no event shall the owner of the copyrights, or the authors of the applications/code be liable for any loss of profit, any problems or any damage resulting from the use or evaluation of the applications/code.