In this article, we will learn How to calculate the weighted average in Excel.
Weighted Average in mathematics:
Weighted average is a kind of arithmetic mean in which some elements of the data set carry more importance than others. In other words, each value to be averaged is assigned a certain weight.
Normal Average = Sum of values in a range / number of values in a range
In mathematics and statistics, you calculate the weighted average by multiplying each value in the set by its weight, then you add up the products and divide the products' sum by the sum of all weights.
Weighted average = score1 * weight1 + score2 * weight2 + . . . + Score5 * weight5 / sum of all weights
In any example, in order to calculate the weighted average (overall grade), you multiply each grade by the corresponding percentage (converted to a decimal), add up the 5 products together, and divide that number by the sum of 5 weights:
Calculate weighted average in Excel
In excel, we can calculate the weighted average of the database using 3 different excel functions.
Let's learn each process one by one to understand how the weighted average is calculated.
Example :
All of these might be confusing to understand. Let's understand how to use the function using an example. Here we have a list of values and its respective weightage. As we understand from the formula we can calculate the weighted average simply just by using a simple formula shown and explained below.
Use the formula:
| =(C2*D2+C3*D3+C4*D4)/(D2+D3+D4) |
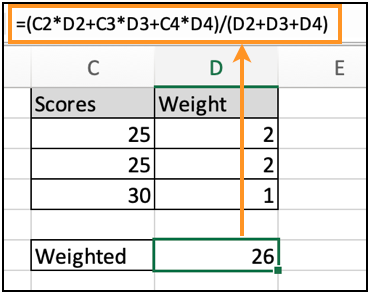
As you can see, the weighted average comes out to be 26. This manual process is easy till the range of values are less. When we calculate the weighted average even for 20 values at once, this process becomes lengthy and hectic and can also lead to mistakes.
Weighted average using SUM function and SUMPRODUCT function
The above excel function mentioned will help in making our calculations easier. The numerator part of the formula will be handled by SUMPRODUCT function and denominator part will be handled by SUM function.
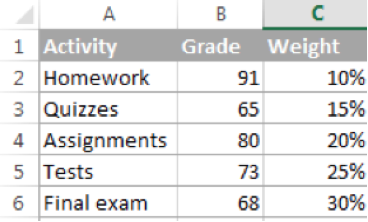
Here we have two arrays : Scores or Grades obtained in each activity and weightage of each activity
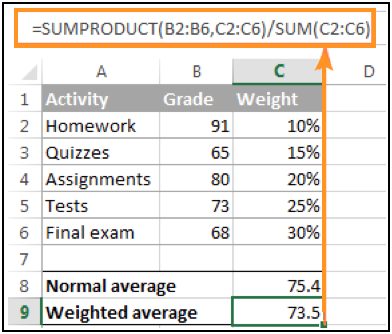
Use the formula in the cell to find the weighted average
| =SUMPRODUCT(B2:B6,C2:C6) / SUM(C2:C6) |
Press Enter to get the weighted sum of the data.

Explanation:
SUMPRODUCT function calculates the sum of the products of corresponding values (Score * Weightage(score)) and SUM function finds the sum of Weightage.
As you can see, the clear difference between the average and weighted average for the same range of values. The concept of average comes from mathematics. Average can be defined as the result that we obtain after adding several quantities and then dividing this total by the number of quantities.
The weighted mean is similar to the arithmetic mean where instead of each of the data points contributing equally to the final average, some data points contribute more than others.
Here are all the observational notes using the formula in Excel
Notes :
Hope this article about How to calculate weighted average in Excel is explanatory. Find more articles on calculating values and related Excel formulas here. If you liked our blogs, share it with your friends on Facebook. And also you can follow us on Twitter and Facebook. We would love to hear from you, do let us know how we can improve, complement or innovate our work and make it better for you. Write to us at info@exceltip.com.
Related Articles :
How to use the AVERAGEIF function in Excel : This function takes the average of values in range applying any one condition over the corresponding or the same range.
How to use the AVERAGEIFS function in Excel : This function takes the average of values in range applying any multiple conditions over the corresponding or the same range.
How To Highlight Cells Above and Below Average Value : highlight values which are above or below the average value using the conditional formatting in Excel.
Ignore zero in the Average of numbers : calculate the average of numbers in the array ignoring zeros using AVERAGEIF function in Excel.
Calculate Weighted Average : find the average of values having different weight using SUMPRODUCT function in Excel.
Average Difference between lists : calculate the difference in average of two different lists. Learn more about how to calculate average using basic mathematical average formula.
Average numbers if not blank in Excel : extract average of values if cell is not blank in excel.
AVERAGE of top 3 scores in a list in excel : Find the average of numbers with criteria as highest 3 numbers from the list in Excel
Popular Articles :
50 Excel Shortcuts to Increase Your Productivity : Get faster at your tasks in Excel. These shortcuts will help you increase your work efficiency in Excel.
How to use the VLOOKUP Function in Excel : This is one of the most used and popular functions of excel that is used to lookup value from different ranges and sheets.
How to use the IF Function in Excel : The IF statement in Excel checks the condition and returns a specific value if the condition is TRUE or returns another specific value if FALSE.
How to use the SUMIF Function in Excel : This is another dashboard essential function. This helps you sum up values on specific conditions.
How to use the COUNTIF Function in Excel : Count values with conditions using this amazing function. You don't need to filter your data to count specific values. Countif function is essential to prepare your dashboard.
The applications/code on this site are distributed as is and without warranties or liability. In no event shall the owner of the copyrights, or the authors of the applications/code be liable for any loss of profit, any problems or any damage resulting from the use or evaluation of the applications/code.