In this article, we will learn about how to use the IMEXP function in Excel.
COMPLEX number (inumber) in excel derived for mathematical number having real and imaginary coefficients. In mathematics we call it the coefficient of i or j (iota).
i = (-1)1/2
Square root of negative number is not possible, so for calculation purpose, ?-1 is named as imaginary and call it iota (i or j). For calculation of some term like shown below.
A = 2 + (-25)1/2
A = 2 + (-1 * 25)1/2
A = 2 + (-1 * 5 * 5)1/2
A = 2 + 5 * (-1)1/2
X + iY = 2 + 5i
This here equation is a Complex number (inumber) having 2 different parts called real part & imaginary part
The coefficient of iota (i) which is 5 is called as imaginary part and the other part 2 is called the real part of the complex number.
Complex number (inumber) is written in the X + iY format.Complex exponential of a complex number (X + iY) is given by.
e( X + iY) = eX * eiY = eX ( Cos ( y ) + i Sin ( y ) ) (complex exponential)
Here X & Y are the coefficients of the real & imaginary part of the complex number (inumber).
Here:
The IMEXP function returns the complex exponential of the complex number (inumber) having both real & imaginary part.
Syntax:
inumber : complex number for which you want the complex exponential.
Let’s understand this function using it in an example.
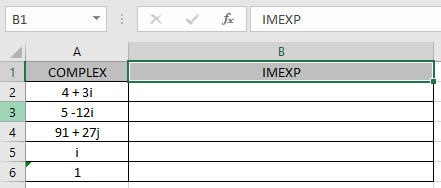
Here we have values where we need to get the complex exponential of the input complex number (inumber)
Use the formula:
A2 : complex number (inumber) provided as cell reference.
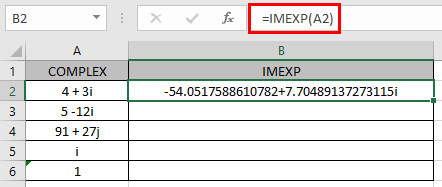
As you can see the complex number having real_num = 4 & imaginary part = 3. The formula returns the complex exponential of the complex number. The coefficient’s sign of i (iota) is changed.
COMPLEX exponential (4 + 3i) = eX (Cos (3) +i Sin(3))
Now copy the formula to the other remaining cells using Ctrl + D shortcut key.

As you can see the IMEXP function formula giving results just fine.
The table show here explains more about the results
| inumber | Real part (X) | Imaginary part (Y) |
| i = 0 + 1i | 0 | 1 |
| 1 = 1 + 0i | 1 | 0 |
Note:
The formula returns the #NUM! error if the complex number doesn’t have lower case i or j (iota).
Hope you understood how to use IMEXP function and referring cell in Excel. Explore more articles on Excel mathematical functions here. Please feel free to state your query or feedback for the above article.
Related Articles
How to use the IMCONJUGATE Function in Excel
How to use the IMSIN Function in Excel
How to use the IMSUM Function in Excel
How to use the IMSUB Function in Excel
How to use the SQRT Function in Excel
How to use the IMARGUMENT Function in Excel
How to use the IMCOS Function in Excel
Popular Articles:
50 Excel Shortcuts to Increase Your Productivity
How to use the VLOOKUP Function in Excel
How to use the COUNTIF in Excel 2016
How to use the SUMIF Function in Excel
The applications/code on this site are distributed as is and without warranties or liability. In no event shall the owner of the copyrights, or the authors of the applications/code be liable for any loss of profit, any problems or any damage resulting from the use or evaluation of the applications/code.