While performing the calculation to ignore the blank cells we will use ISNUMBER, AND and IF formulas in Microsoft Excel.
ISNUMBER: This function can be used to check if a cell contains a number.
For Example:-
IF: -IF condition allows us to use multiple conditions in a cell. It helps us to make the function flexible and Excel allows upto a max of 64 conditions which can be checked in a cell.
Example:Cells A2 and A3 contain the numbers 3 and 5. If the cell contains 3, then the formula should display “Yes” otherwise “No”.
=IF (A1=3,"Yes","No")

AND: This function is an operator function and is used to combine multiple criteria for a cell
Example:Column A contains 3 numbers. We need to check if these numbers are greater than 10 and less than or equal to 50.
=AND(A1>10,A1<=50)

2 of the cells have numbers which are not greater than 10 AND less than or equal to 50. Hence they show as False, while the last number has a True result.
Let’s take an example and understand how you can ignore blank cells when performing calculations.
We have 2 lists in columns A & B, in which some cells are containing numbers and some cells are blank. In this example we need to multiply the numbers from the corresponding cells in both the columns. Our condition is that if any cell among the two is blank, the formula should give a blank result, else it should multiply the numbers in both the cells.

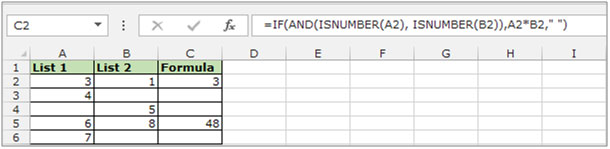
We find that once the formula has been copied to the whole column, only cells C2 and C5 show the result, while C3, C4 and C6 are blank as any of the cells in these rows are blank.
In this way you can use this formula to ignore the blank cells while the calculation is performed.
If you liked our blogs, share it with your friends on Facebook. And also you can follow us on Twitter and Facebook.
We would love to hear from you, do let us know how we can improve, complement or innovate our work and make it better for you. Write us at info@exceltip.com
The applications/code on this site are distributed as is and without warranties or liability. In no event shall the owner of the copyrights, or the authors of the applications/code be liable for any loss of profit, any problems or any damage resulting from the use or evaluation of the applications/code.
I have 3 rows of numbers with blank cells staggered as below ,how do i dynamically transpose the 3 rows into a single column ignoring the blank cells with a formula
1 21 30 53 60
18 36 43 63 70
4 38 54 71 81
Thanks
Hi arvind,
the transpose function in excel can be used to transpose any matrix. But the transpose function is matrix function and does not deal with the values of the cell, so you will not be able identify the blank cells. You can first delete the blank cells and then transpose or wise versa.
I'm building a sheet to calculate GPAs and I'm having difficulty trying to add the values in a group of cells =SUM(IF(ISBLANK(I16:I28),I16:I26,I16:I28)) that also include two blank cells (I27, I28) that normally have no values and reflect #value because they are blank.
88 3.25 3.250 B+
92 3.5 3.500 A-
91 3.5 3.500 A-
__ __ #VALUE! __
__ __ #VALUE! __
if the cell contains #VALUE ERROR and you want to identify it, use the ISERROR function instead of ISBLANK. However, the best solution for you would be the AGGREGATE FUNCTION. You can customize your results and tell excel to ignore blank cells or errors. https://www.exceltip.com/mathematical-functions/how-to-use-excel-aggregate-function.html
Hi- I'm using this formula in cell I42: =IF(I$43<$I42,"Y","N") along with conditional formatting in that same cell (I42) if answer is "Yes" format cell green; If "No" format cell red. My problem is the cell where this formula sits "pre populates with a red N even though there is No data in I42. Do you have any suggestions?
Use this formula
=IF(I42="","",IF(I$43<$I42,"Y","N")) or IF(ISBLANK(I42),"",IF(I$43<$I42,"Y","N"))
Hi, I am using the formula =IF(A11=0,"Out Of Stock", "") on an invoice but how do i make it ignore if cell is blank?
So I'm trying to divide column F, by column C. However it keeps reading the blank cells as 0 and trying to divide them. I'm sure its something simple that I am just missing, but I cant seem to find it.
I am trying to track the sales I make. So if I buy something for $100, sell it for $125, but I pay shipping so -$5, and I pay tax -$1, my total income or revenue is $19. I can make that all work.. but what I want is for the income or revenue box to show -$100 until the other boxes have calculations in them. Help!
You can postpone calculation in in income cell using a formula that may look like this,
=IF(OR(ISBLANK(buy_something),ISBLANK(sell),ISBLANK(payshipping)...),-buy_something, your calculation)
it will show a negative value of the purchased item in the income cell until you have all the cells filled up.
Hi there!
I'm using excel to keep track of inventory, price, selling fees and profit of sold items. I've managed to figure out how to add all the profits column together, but each row is an item I have in stock and I want to be able to have it take my sale price - item cost - seller fee to give me my profit per item and if there is no seller fee to not give me my profit (since that item hasn't sold). I hope that makes sense. I can send a screenshot if it doesn't.
Thanks in advance for your assistance!
You can use a formula based on IF and ISBLANK.
=IF(ISBLANK(seller_fee),no_profit, profit_calculation)
On the place of seller fee, give reference of seller fee cell. At no_profit write your calculation that does not give you profit. At profit_calculation put formula that returns the profit.
I hope this helps.
Hi,
I am trying to calculate the price difference between weeks, however some cells are left blank as that week there was no price update. How am I able to extend this formula to ignore if a "week"is blank to go to the following week?
Example: =IF(AND('DATA EXTRACT'!Z2'DATA EXTRACT'!Y2),'DATA EXTRACT'!Z2-'DATA EXTRACT'!Y2,"No Change")
Provider Country of Origin Port of Loading Country of Destination Port of Discharge WK 51 WK 52 WK 01 WK 02 WK 03 WK 04
#### #### #### #### #### $850.00 $850.00 $500.00 $200.00
Thank you,
Hi
I use the following formula to show how long i have left to complete a piece of work IF(S6>0,S6-$B$3," ").
Is there a way to ignore the formula if a cell in column S is blank? All cells where Column S is blank show #VALUE!
Thanks
Hi,
You can use the formula, IF(ISBLANK(76),"",IF(S6>0,S6-$B$3," ")).
Hi,
i need a little help with this formula for my car road map: =IF(OR(H21=7,H21=6)," ",D20)
H21 = weekdays and 6&7 are Saturday and Sunday
D20= are the last km made
The problem comes after the week end, the cell for monday will bring the value "0", because i have 2 blank cells between :(. How can i do, to take the last cell with value in the column D.
Thx in advance.
I have a formula grabbing the numbers at the end of a cell and my stores sales are spaced by 4 rows that I need to ski. What would be my IF solution for =RIGHT(E4,FIND(" ",E4)-1)
I have multiple numbers in row with some blank cells in between, how do i take these numbers to another file, without blank cells.
Praveen, you can use filter or go to special method to copy non-blank cells to new range. It is explained here:
https://www.exceltip.com/basic-excel/select-and-copy-only-non-blank-ranges-in-excel.html
01/01/1937 01/01/1975 38 Years, 0 Months, 0 Days
01/01/1976 01/01/1977 1 Years, 0 Months, 0 Days
01/01/1977 29/11/1986 9 Years, 10 Months, 28 Days
01/10/1988 01/01/1990 1 Years, 3 Months, 0 Days
01/11/2017 117 Years, 10 Months, 1 Days
I am using the following formula to calculate the date range of 2 date columns
=DATEDIF(D2,E2,"Y") & " Years, " & DATEDIF(D2,E2,"YM") & " Months, " & DATEDIF(D2,E2,"MD") & " Days"
What I need is to ignore blank cell calculations, tried variations of ISBlank but getting nowhere "Help"
also need to sort largest (Elapsed YMD) to smallest, thanks in advance.
I'm using a formula to calculate my daily word count. I have multiple stories I might be working on, so each story has it's own column and I calculate the daily word count by subtracting yesterday's word count in each column from today's word count and adding them up as follows:
=if(and(isblank(C7), isblank(D7), isblank(E7)), "", IF(not(isblank(C7)), C7-C6) + if(not(isblank(D7)), D7-D6) + if(not(isblank(E7)), E7-E6))
This works well as long as I have a number in the previous day's row. What I want it to do though is subtract from the last row that has a number. For example:
Jan 1: 800
Jan 2: 1200
Jan 3:
Jan 4: 1600
In the above, Jan 2 it understands I wrote 400 words (Jan 2 - Jan 1), and Jan 3 it understands I wrote 0 words (because I tell it to ignore if blank), but on Jan 4 it thinks I wrote 1600 words (Jan 4 - Jan 3). I want Jan 4 to instead subtract the last row to have a number it in instead of just the previous column (so in this case Jan 4 - Jan 2).
I hope this makes sense. I've been having trouble Googling it because I can't figure out how to explain what I'm trying to do.
Thanks!
PLEASE HELP: I have the following formulas in two separate cells. They are identical other than the cells they are adding, but the first formula errors and the second one works perfectly. I have found a different formula that will give the correct result, but will input "0" if the answer is zero and I want it to stay blank if zero is the result. Originally, I thought the issue was the in one of the cells included in the first formula was blank, so it didn't know how to add one cell with a blank cell, but currently, all cells in the "AA" column are blank so everything is consistent.
=IF(SUM(AA9+AA11)=0,"",SUM(AA9+AA11))
=IF(SUM(AA7:AA8,AA10,AA12:AA23)=0,"",SUM(AA7:AA8,AA10,AA12:AA23))
Hi,
I am trying to write a formula which identifies if data complies with a set of values but I want the calculation cell to be blank if there is no data in the cell.
So far I have =IF(AND(I13>=0.5,I14<=2),"Y","N"
What will I need to add for the calculating cell to be left blank if the data cell is also left blank?
Thanks in advance for your help.
"You can use this formula,
=IF(OR(ISBLANK(I13),ISBLANK(I14)),"""",IF(AND(I13>=0.5,I14<=2),""Y"",""N"")) This will check both cells, if any of'em is empty it will show nothing else your formula will execute. you can use this article https://www.exceltip.com/working-with-formulas/creating-formulas-that-only-return-results-from-non-blank-cells.html"
Hi
I'm running the following array formula to track MAX, MIN and AVERAGE across a range of cells but cannot get it to ignore zeroes/blanks. Any suggestions on how I can amend?
{=MAX(B$24,MAX(IF(MOD(COLUMN(G$24:DH$24)-COLUMN(G$24)+0,5)=0,G$24:DH$24)))}
Thanks
Rod
Hello, i'm trying to get my formula to display nothing when cell J188 is blank however is doesn't work.
Can someone please help? the Holidays is an additional sheet with information on it.
=WORKDAY(J188,K188,Holidays!$A$2:$A$49)
I am using the left function to return anything that is before "-" some of my cells in the column I am referencing are blank and I want it to just return a blank and not #Value
Here is my formula =LEFT(O2,SEARCH("-",O2)-1)
"Hi,
use an if statement to check blank.
=IF(ISBLANK(O2),"""",LEFT(O2,SEARCH(“-”,O2)-1))"
Hello!
I am trying to add rules to the formula where if the first field is blank, then it won't do the calculation. But if it is not blank, then to complete the calculation.
The calculation I am using is: =-G10*F11+G10
So if F11 is blank, do not provide a result
If F11 has a figure, complete the result.
Thank you
I am trying to get a cell to add one day to the date in A5 (=A5+1), but return nothing if A5 is blank. Anyone know how?
Hi Tovah,
Use this formula
=IF(ISBLANK(A5),"",A5+1)
I am trying to formulate averages of multiple cells, but in some cells in the row there is no value. I keep getting the #DIV/0! Error. How do I make it give the average while ignoring the blank cells? Thanks!!
Hi! How can i make this formula to show me the result if one or more of the cells in the formula are blank?
I have the following formula in my excel and i don't know exactly how to make it show me the result:
=IF(AND(ISNUMBER('31'!I8),ISNUMBER('30'!I8),'31'!I8+'30'!I8)
it shows me only true or false because one of the cells are blank
Thank you in advance for your help
Thanks for this tip,
I tried dozens of formulas unsuccessfully but your's work. I was adding contiguous cells on each of hundred rows to then obtain an average of the sums. Some formulas returned unwanted zeros or blanks. I just wanted zeros if the sum really returned zeros or blanks if the rows were empty.
However, it caused an unwanted situation. I have an Index to identify the highest value of the sums highlighting the corresponding range row. Now I have alternated highlighted rows in the blank or empty rows (all the rows have alternated fill as a visual aid). How can I fix this thing?
Thanks, need to put an ABS formula in here as well to work out difference between L2-K2 but with no negative values but i cannot get it to work. Any idea?
=IF(AND(ISNUMBER(I2), ISNUMBER(K2)),I2-K2,” “)
=IF(AND(ISNUMBER(I2), ISNUMBER(K2)),=ABS(I2-K2,” “))
Thanks, John
My current formula is to compare goals scored in a football game. =IF(M3=P3,1,0) is the formula I'm using to calculate a draw, how do I change this to produce a blank result if either/both M3 & P3 are blank?
Hey Dean,
use this formula
IF(OR(M3=””,P3=””),IF(M3=P3,1,0))
I have a formula to calculate time as follows, where C9 is 8:00am and D9 is 6:00PM:
=IF(D9>C9,D9-C9,1-(C9-D9))
This returns a value of 10.
I want to edit the formula to return a blank cell if C9 and D9 were empty.
Help me!!??
Hi Jenna,
if you want to return a blank cell if any of C9 and D9 is empty then write this formula.
=IF(OR(D9="",C9="")," ",IF(D9>C9,D9-C9,1-(C9-D9)))
if you want to return a blank cell if both C9 and D9 are empty then write this formula.
=IF(AND(D9="",C9="")," ",IF(D9>C9,D9-C9,1-(C9-D9)))
Hi, I'm working with something similar, but want it to return a zero if the second cell is blank. Formula I'm using is:
=IF(OR(N2=" ",O2=" "),0,DATEDIF(N2,O2,"D"))
Because I have a date in one column it returns #NUM error.
Help?
You may find that just removing the space tab between " " ie to "" resolves the problem. Seems to work on my excel