In this article, we will learn How to use matrix and matrix calculations in Excel.
Scenario
A computer spreadsheet is a series of small blocks (cells) where the columns are labeled with capital letters and the rows are labeled by numbers. To enter a matrix into Microsoft Excel, simply type each matrix element into its own small block (cell). Let's learn what are different matrix properties and perform operations in excel.
Matrix Addition and subtraction
Let A and B be r × c matrices with A = [aij] and B = [bij]. Then A + B is an r × c matrix with A + B = [aij + bij] and A – B is an r × c matrix with A – B = [aij – bij].
Definition 2: A matrix can be multiplied (or divided) by a scalar. A scalar can also be added to (or subtracted from) a matrix.
Let A be an r × c matrix with A = [aij] and let b be a scalar. Then bA and A + b are r × c matrices where bA = [b · aij] and A + b = [aij + b]. We can define Ab and b + A in a similar fashion. Clearly, b + A = A + b and Ab = bA. Division and subtraction of matrices by scalars can be defined similarly.
Matrix Multiplication
Let A be a p × m matrix with A = [aij], and let B be an m × n matrix with B = [bjk]. Then AB is an p × n matrix with AB = [cik] where
![]()
For the multiplication AB to be valid, the number of columns in A must equal the number of rows in B. The resulting matrix will have the same number of rows as A and the same number of columns as B.
The associative law holds, namely (AB)C = A(BC), i.e. it doesn’t matter whether you multiply A by B and then multiply the result by C or first multiply B by C and then multiply A by the result. It is essential that the matrices have a compatible shape. Thus if A is p × m, B is m × n and C is n × s then ABC will have shape p × s. The distributive laws, namely A(B + C) = AB + BC and (A + B)C = AC + BC, also hold.
The commutative law of addition holds, namely A + B = B + A, but the commutative law of multiplication does not hold even when the matrices have a suitable shape; thus, even for two n x n matrices A and B, AB is not necessarily equal to BA. For square matrices, the trace of AB is equal to the trace of BA though.
For square matrices A and B of the same size and shape and scalar c:
A (square) matrix A is symmetric if A = AT
Property 1:
Non singular matrix
An n × n matrix A is invertible (also called non-singular) if there is a matrix B such that AB = BA = In. A-1 is the inverse of A provided AA-1 = A-1A = In. A matrix which is not invertible is called singular.
If A is invertible, then the inverse is unique.
Suppose B and C are inverses of A. Then by the associative law, C = IC = (BA)C = B(AC) = BI = B, and so C = B.
Observation: In fact, if there is a matrix B such that AB = In or BA = In then A is invertible and A-1 = B.
Property 3: If A and B are invertible, then (A-1)-1 = A and (AB)-1 = B-1 A-1
Since (AB)(B-1A-1) = A(BB-1)A-1,= AIA-1 = AA-1 = I the second assertion follows from the second assertion of Property 2.
Property 4: If A is invertible, then so is its transpose and (AT)-1 = (A-1)T
AT(A-1)T = (A-1A)T = IT = I. Similarly, (A-1)TAT = (AA-1)T = IT = I.
Property 5: A is symmetric if and only if A-1 is also symmetric
Let's assume A is symmetric, then by Property 4, (A-1)T = (AT)-1 = A-1, and so A-1 is also symmetric. For the converse, assume that A-1 is symmetric, then from the above, it follows that (A-1)-1 is symmetric, but by Property 3, this means that A is symmetric.
Find the inverse of
![]()
Since the inverse of A takes the form
![]()
where AA-1 = I2, it follows that
![]()
Thus we need to solve the following four linear equations in four unknowns:
![]()
![]()
![]()
![]()
Solving these equations yields a = 2/3, b = -1/3, c = 1/3, d=1/3, and so it follows that
![]()
Excel matrix Functions:
Excel provides the following array functions to carry out the various matrix operations described above (where we conflate the arrays A and B with the ranges in an Excel worksheet that contain these arrays).
MMULT(A, B): If A is an p × m array and B is an m × n array, then MMULT(A, B) = the p × n matrix AB. Note that since this is an array function, you must first highlight a p × n range before entering =MMULT(A, B) and then you must press Ctrl-Shift-Enter.
MINVERSE(A): If A is an n × n square array, then MINVERSE(A) = A-1. This is an array function and so you must highlight an n × n range before entering
=MINVERSE(A) and then pressing Ctrl-Shift-Enter.
TRANSPOSE(A): If A is an m × n array, then TRANSPOSE(A) = AT. This is an array function and so you must highlight an n × m range before entering =TRANSPOSE(A) and then pressing Ctrl-Shift-Enter.
Versions of Excel starting with Excel 2016 also provide the array function MUNIT(n) which returns the n × n identity matrix.
You can also transpose an array A in Excel by copying the array (i.e. by highlighting the array and pressing Ctrl-C), clicking where you want AT located (i.e. the cell at the upper left corner of AT) and then selecting Home > Clipboard|Paste and choose the Transpose option.
In addition, if A and B are defined as arrays (e.g. they are named arrays or entities such as B5:F8 or they are the results of matrix operations such as TRANSPOSE, INVERSE or MMULT, then they can be manipulated using the +, -, *, / and ^ operators. These operations are done on a cell by cell basis.
Note too that if A is an m × n matrix and B is a 1 × n matrix (i.e. a row vector) then A + B is a valid operation in Excel and gives the same result as A + C where C is an m × n matrix all of whose rows contain the same data as B. Similarly you can calculate A – B, A*B and A/B. Also, you can calculate A + B, A – B, A*B and A/B where B is an m × 1 column vector.
Real Statistics Data Analysis Tool: The Real Statistics Resource Pack provides the Matrix Operations data analysis tool, which supports a number of matrix operations. These work just like the corresponding worksheet array functions TRANSPOSE, MINVERSE, etc., except that you don’t need to specify the shape and size of the matrix since these are determined automatically from the shape and size of the input matrix.
Example 2: Perform all the operations supported by the Matrix Operations data analysis tool for the matrix in range A3:C5 of Figure 1.
After pressing Ctrl-m and selecting the Matrix Operations option (from the Desc tab if using the MultiPage user interface), a dialog box appears as shown on the right side of Figure 1. Next, click on all the options as shown in the figure.

Figure 1 – Data and dialog box for Example 2
After clicking on the OK button, the results shown in Figures 2, 3, 4 and 5 appear (slightly reformatted).
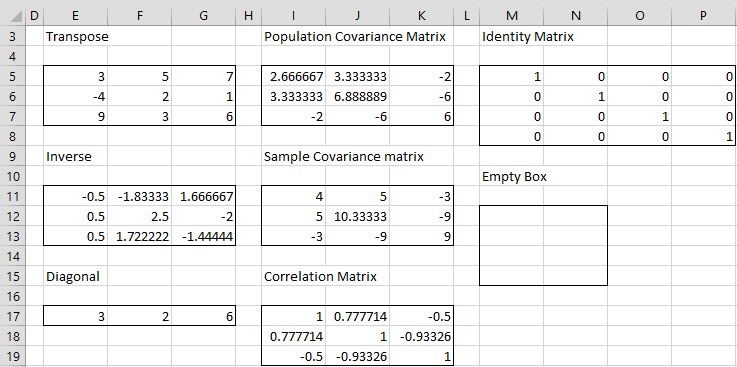
Figure 2 – Output from Matrix data analysis tool (part 1)
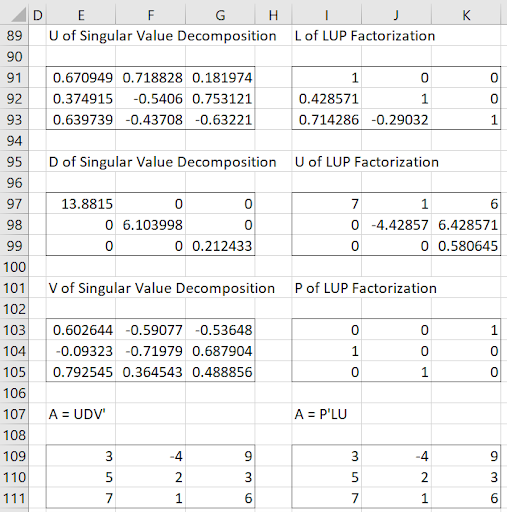
Figure 3 – Output from Matrix data analysis tool (part 2)

Figure 4 – Output from Matrix data analysis tool (part 3)

Figure 5 – Output from Matrix data analysis tool (part 4)
Definition 6: Vectors X1, …, Xk of the same size and shape are independent if for any scalar values b1, … bk, if b1 X1 +?+ bk Xk = 0, then b1 = … = bk = 0.
Vectors X1, …, Xk are dependent if they are not independent, i.e. there are scalars b1, … bk, at least one of which is non-zero, such that b1 X1 +?+ bk Xk = 0.
Observation: If X1, …, Xk are independent, then Xj ? 0 for all j.
Property 6: X1, …, Xk are dependent if and only if at least one of the vectors can be expressed as a linear combination of the others.
Proof: Suppose X1, …, Xk are dependent. Then there are scalars b1, … bk, at least one of which is non-zero such that b1 X1 +?+ bk Xk = 0. Say bi ? 0. Then
![]()
Definition 7: The dot product of two vectors X = [xi] and Y = [yj] of the same shape is defined to be the scalar
![]()
Observation: If X and Y are n × 1 column vectors, then X?Y = XTY = YTX. Also ||X|| = ?X·X.
Excel Function: If R1 is the range containing the data in X and R2 is the range containing the data in Y then X · Y = SUMPRODUCT(R1, R2).
Definition 8: Two non-null vectors of the same shape are orthogonal if their dot product is 0.
Many of the Microsoft Excel functions that you will be using to complete these matrix operations are array functions – returning more than one value at a time. To enter an array function into a Microsoft Excel worksheet, you must hold down the CTRL and SHIFT keys while pressing the ENTER key: CTRL+SHIFT+ENTER. Once this is done, braces will surround the array formula.
Hope this article about How to use matrix and matrix calculations in Excel is explanatory. Find more articles on calculating values and related Excel formulas here. If you liked our blogs, share it with your friends on Facebook. And also you can follow us on Twitter and Facebook. We would love to hear from you, do let us know how we can improve, complement or innovate our work and make it better for you. Write to us at info@exceltip.com.
Related Articles :
How to use the MUNIT function in Excel : Extract Unit or identity matrix using MUNIT function in excel. Click the link to learn more.
How to use the MINVERSE function in Excel : Extract Inverse of a matrix using MINVERSE function in excel. Click the link to learn more.
How to use the MDETERM function in Excel : Extract determinant of a matrix using MDETERM function in excel. Click the link to learn more.
How to use the TRANSPOSE function in Excel : Extract TRANSPOSE (rows > columns & columns > rows) of a matrix using TRANSPOSE function in excel. Click the link to learn more.
Popular Articles :
50 Excel Shortcuts to Increase Your Productivity : Get faster at your tasks in Excel. These shortcuts will help you increase your work efficiency in Excel.
How to use the VLOOKUP Function in Excel : This is one of the most used and popular functions of excel that is used to lookup value from different ranges and sheets.
How to use the IF Function in Excel : The IF statement in Excel checks the condition and returns a specific value if the condition is TRUE or returns another specific value if FALSE.
How to use the SUMIF Function in Excel : This is another dashboard essential function. This helps you sum up values on specific conditions.
How to use the COUNTIF Function in Excel : Count values with conditions using this amazing function. You don't need to filter your data to count specific values. Countif function is essential to prepare your dashboard.
The applications/code on this site are distributed as is and without warranties or liability. In no event shall the owner of the copyrights, or the authors of the applications/code be liable for any loss of profit, any problems or any damage resulting from the use or evaluation of the applications/code.